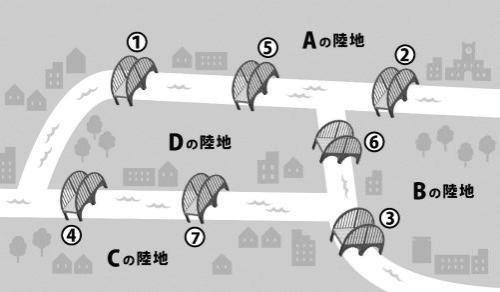
ときは18世紀、ケーニヒスベルクという街で「町中の橋を1回ずつ通ることができるかどうか」という議論が盛り上がりました（図1参照）。
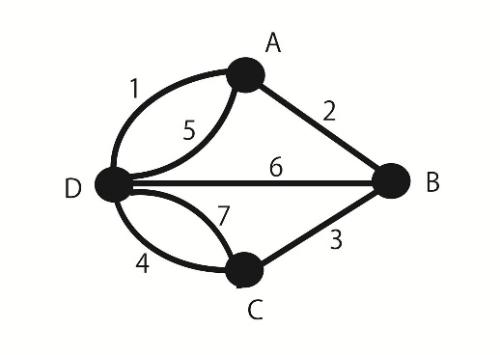
　これに答えたのは数学者のオイラー。地図を図形に置き換え、数学の一筆書きの問題として考えました。彼は、一筆書きが可能となる条件が「奇数個の辺と接続する頂点の数が、0または2」と証明し、この問題は条件を満たさないため一筆書きは不可能と示しました（図2参照）。
　現代に当てはめると、新しい街を散策する時に全ての通りを歩く最短経路を考えることに相当します。「全ての通りを歩くのは大変だから、観光名所だけを巡る最短経路が知りたい！」という方、これも図形に置き換えて考えられるのでぜひ挑戦してください。でもこれにはオイラー先生も苦戦するかも…「全ての観光名所を巡る最短経路を効率よく探す問題」は、実は100万ドルの懸賞金付きの未解決問題なのです。
　この夏、観光地を訪れたら、複数の名所を一筆書きで巡ることができるか、皆さんも試してみてはいかがでしょうか。
（市報　平成27年8月1日号掲載）

［写真：ケーニヒスベルクの街］

［写真：オイラーの証明］